

Instructions for:
Pulleys

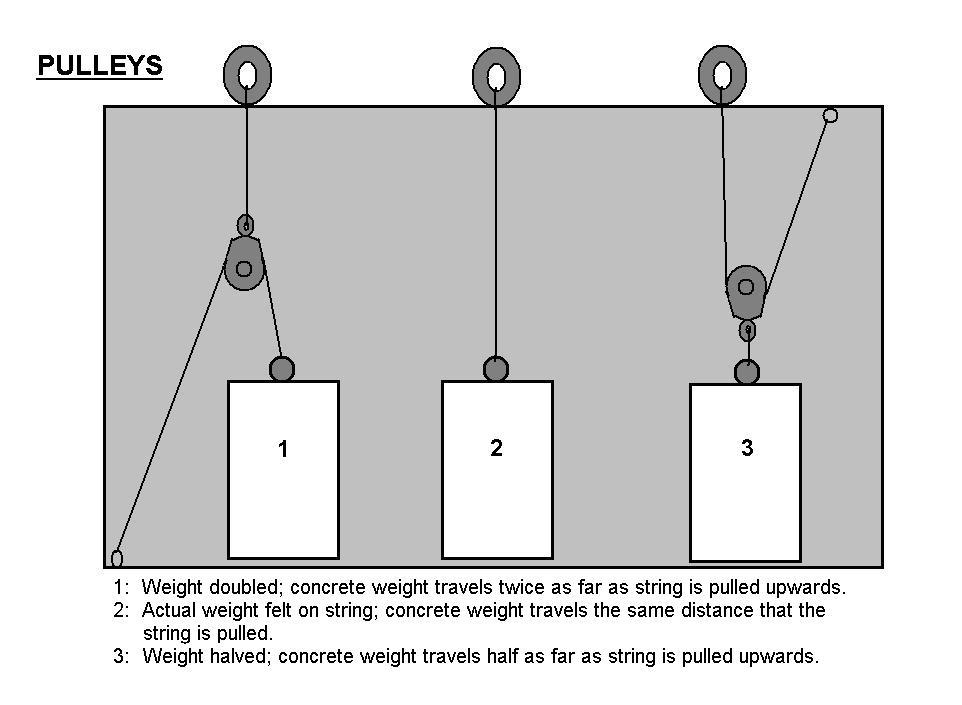
This station involves three different arrangements of pulleys and ropes, each attached to, and lifting an identical concrete weight.
Click to enlarge image
Let students investigate the Pulleys demonstration on their own. The following questions are helpful.
Questions for Students / Items of Interest:
Q1) Do all the concrete weights weigh the same? (pick them up directly)
Q2) Do they all weigh the same when you use the pulleys? (use the washer/string to lift the weights) Which one feels heaviest? Lightest?
Q3) Considering this, how far do you have to pull each string to lift the weight to the top of the pulley box? How far do you have to pull the "heavy" weight string? How far do you have to pull the "light" weight string?
For more advanced studies, one can look at how the concept of work comes into play in this demonstration.
Work is defined as motion in the direction of a force. Work is done to pull the pulleys upward, as a studentís hand creates an upward force that lifts the weight. This can be quantified in the formula: Work = Force x Distance (W= Fd). If we were to forgo the pulleys altogether, and lift the weights directly, we would expect that it would take the same amount of work to lift each pulley to the top of the pulley box. Indeed, this is the case when lifting with the pulleys too. The first arrangement involves a doubling of the applied force, but a halving of the distance needed to lift the weight. The last arrangement is just the opposite, dividing the needed force by two, but requiring twice the pulling distance. Each of these concrete weights has a mass of about one kilogram (about 10 Newtons of force), and the distance the weight must travel to reach the top of the box is around 10 centimeters, so letís calculate the work done in each arrangement to lift the pulley to the top of the box.
For the first arrangement, the force felt is doubled, so a 20 Newton force must be applied by the student to lift the weight. However, the distance the string must be pulled to lift the pulley to the top is halved, only 5 centimeters (0.05m). The work done:
W = Fd = (20 N) (0.05 m) = 1 Joule
For the middle arrangement, the distance and force applied are the same as lifting the weight directly; a 10 N force acting across 10 cm (0.1m):
W = Fd = (10 N) (0.1 m) = 1 Joule
The last arrangement is the opposite of the first, with a halved force (5 N) and a double distance (20 cm or 0.2 m). The work done:
W = Fd = (5 N) (0.2 m ) = 1 Joule
The work done in each case, expressed in Joules (the metric unit of energy and work) is equal regardless of pulley arrangement. This is an interesting look at mechanics. While the amount of work done to accomplish a certain task (i.e. lifting a heavy weight) cannot be changed, the means of doing so certainly can, by using different combinations of forces and distances. Other pulley arrangements (involving more than one pulley) would provide even great force or distance multiplications, creating more options for lifting the weight. Let students consider other pulley arrangements.
Q4) What other simple devices multiply or divide forces to accomplish a task, such as lifting a heavy object?
- Most commonly, the inclined plane and simple lever multiply and divide forces much in the same way a pulley does. By creating mechanical advantage, these devices allow humans to push a refrigerator up a ten foot high ramp, or remove a tightly threaded bolt with a wrench. Discuss other options.
Copyright 2004 Straley/Pinney - The University of Kentucky Physics Petting Zoo