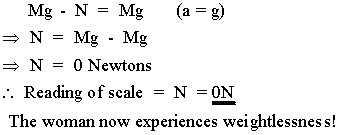Problem 5-44.

Notes:

1. There are only two forces acting on the woman, the weight (Mg, downward) and the normal force N from the scale (upward).
2. The reading of the scale is the magnitude of the normal force (N).
3. These two forces add up to zero only when the elevator and the woman are not accelerating. If the woman is accelerating upward, N has to be larger than Mg and the scale will give a reading larger than the actual weight of the woman. Similarly, if the woman is accelerating downward, she will appear lighter on the scale because N is smaller than Mg.

(b) Again, the elevator is moving with a constant velocity. The answer should be the same as that of part (a). Reading of the scale will be the same as long as there is no acceleration. It does not depend on the velocity of the elevator.

(c )

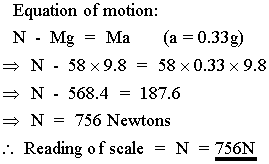
(d)

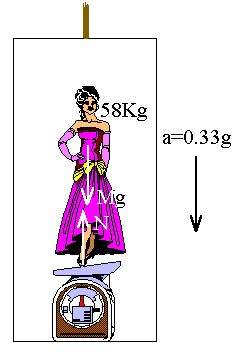
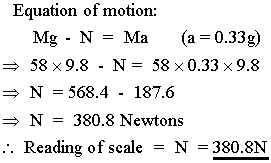
(e) For free fall, a = g downward. The equation of motion will be the same as that of part (d), except with a =g instead of a=0.33g: