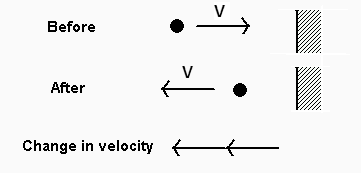
The physics of a moving level
As a subway car leaves the platform, the passengers are advised to hold on. From their point of view, it seems that there is a sudden force that pushes them to the back of the car. Physicists prefer to think of this situation from the point of view of someone standing on the platform: the car has suddenly started moving forwards, and due to inertia the people inside tend to stay where they are.
While the subway car is moving along the tracks, the passengers don't notice the motion, so long as it has constant speed and direction. However, where the track curves, the train changes direction, while the passengers continue in a straight line (if they don't hold on!); from their point of view, it seems that a force has thrown them outwards. Here again, the physicist prefers to discuss this from a fixed point of view: the "outwards" motion is actually a straight-line continuation of the previous motion and there is no outwards force.
A bubble level works the same way as the subway car, with the
liquid inside taking the role of the passengers, and the bubble inside making the liquid's
motion visible. While at rest or moving with constant speed on a level surface, the bubble
is centered; but as the velocity of the level increases, the liquid "gets left behind,"
and so the bubble goes forward.
Likewise, as the velocity decreases, the liquid tries to keep going forward making the bubble
shift backwards, in the direction of the deceleration. In both cases, either positive or
negative acceleration, the bubble moves to one edge of the level, and points in the direction
of the acceleration.
Velocity has both a direction and a magnitude, and changing direction counts as a kind of acceleration.
When a ball bounces off a wall, its speed might not change much but the
direction of motion does. The change in velocity is large and is directed
away from the wall. The bounce doesn't take very long, and so the acceleration
is huge.
For example, if a ball travelling at 10 m/sec bounces back again going
10 m/sec,
change in velocity = 10 m/sec to the left - 10 m/sec to the right
Recall that a velocity to the right can also be represented as a
negative velocity to the left. Then
change in velocity = 10 m/sec to the left - (- 10 m/sec to the left)
= 10 m/sec to the left + 10 m/sec to the left
= 20 m/sec to the left
If the bounce only takes 0.01 sec, the acceleration is 2000
m/sec2 to the left.
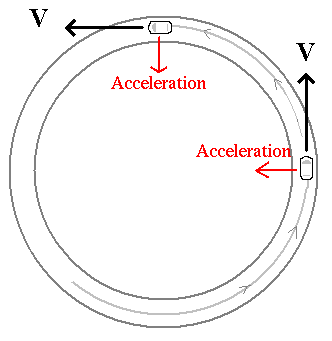
For another example,
consider a car going around a curve, as shown in the drawing.
At one point the car is moving up the screen; later it is moving to the
left. The acceleration is toward the center of the circular
path because that is how the velocity is changing.
We hope that when you moved the level
in a circle, you observed that the bubble tended to point towards the center: this is the
direction of the acceleration for an object moving along a circular path with
constant speed.
The Law of Force and Acceleration
In the second activity, Rolling Downhill, Again, you observed that a steeper hill gives a larger acceleration. This is also the condition under which there is a larger unbalanced force on the ball. This is our first meeting with the Law of Force and Acceleration, which is a quantitative relationship between force and acceleration:
Force = mass x acceleration
It is a part of this law that the direction of the unbalanced force and the direction of the acceleration are the same. If you analyse what you are doing as you move the level around, you will find that the bubble is pointing in the direction you are pushing: forwards, when the level is speeding up; backwards, when it runs into your hand; and towards the center of the circle when you are moving it on a curve. This also explains why you can't use a single barrier to steer a ball in an S shape: the barrier can only push the ball away, and so it must always be on the outside of the curved path of the ball.Check the box when you are done:
Discussion of the second unit on acceleration