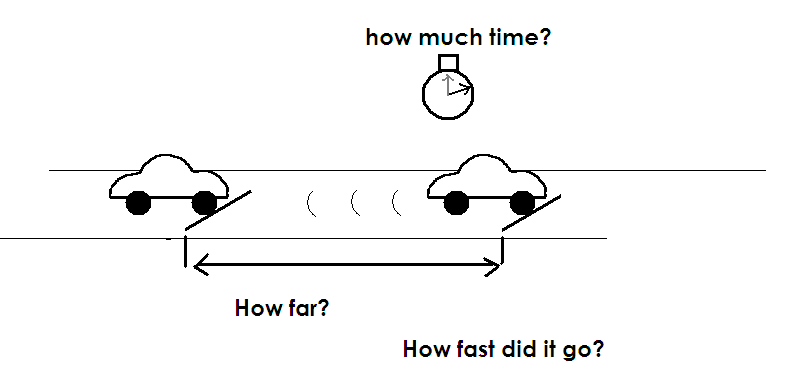Motion is what occurs when something changes its position. Measuring and describing distance, position and time are where we begin our study of motion. Where did an object start? Where did it end up? How far did it go? How long did it take? Force, Motion, and Energy
Force, motion, and energy are closely interrelated. Any one of them could be the starting place for a discussion. The units of this course build understanding of these concepts in a logical sequence while not introducing too many concepts at once. This summary tries to present a more continuous story in greater depth and with more context.
Mass
Mass is a property of an object. It indicates how much matter is present within the object. The unit of mass is the kilogram. At the moment this is defined in terms of a certain lump of metal kept in Paris, France, but in the foreseeable future it will be redefined as the mass of 5.2 x 1025 carbon atoms.
The weight of an object is a measure of how hard the earth’s gravity is pulling on the object. Its weight is proportional to its mass. The proportionality varies so little from place to place on earth that it almost can be represented by a constant (1 Kilogram "equals" 9.8 Newtons). This leads to a source of confusion, in that it suggests that the force of gravity and the mass of the object are the same thing. However, mass is a property of the object itself, while its weight is a property of the interacting system consisting of the Earth and the object. When you visit the moon you will weigh a lot less, allowing you to run up the stairs without losing your breath and lift your dad with one hand, but your mass will be the same and the clothes you wore in high school still will not fit.
Motion
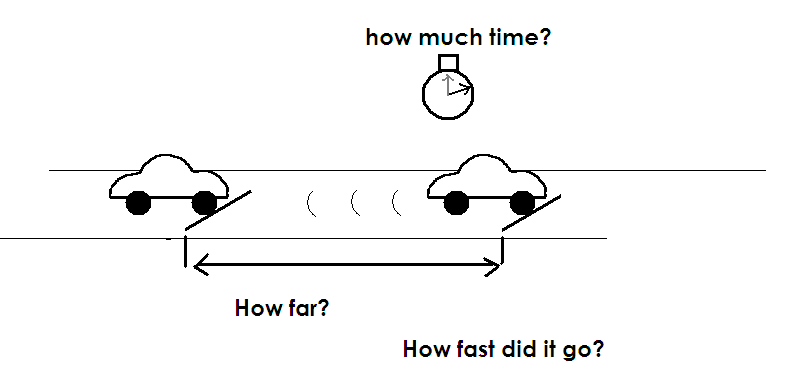Motion is what occurs when something changes its position. Measuring and describing distance, position and time are where we begin our study of motion. Where did an object start? Where did it end up? How far did it go? How long did it take?
A related concept is speed. How fast did it go? Speed is defined as:
Average speed = distance traveled/time elapsed.
It is called "average speed" because it is a property of the whole trip, both the parts when you were speeding down the highway and the parts while you were stopped at the gas station. The car’s speedometer tells us our speed for a short time interval.. When we measure distance in meters and time in seconds, the speed is given in meters per second (m/s).
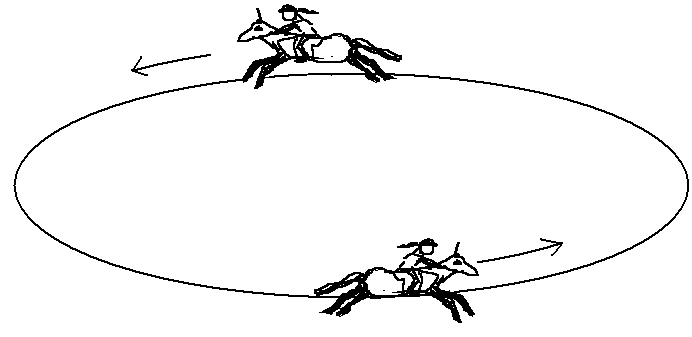Velocity is a related concept, that combines speed and the direction of motion. You can go around a racetrack at constant speed, but you cannot go around at constant velocity, because you have to change direction as you go around.
Constant velocity turns out to be not very exciting from the point of view of the laws of motion, because moving in a straight line at constant speed is what things are supposed to do. Only when we want the velocity to change do we have to do something. The relevant and interesting part of motion is the acceleration, which is the rate of change of velocity:
Acceleration = (final velocity – initial velocity)/time elapsed
Acceleration occurs when there is a change in speed or direction or both. A large acceleration means that velocity is changing rapidly in magnitude or in direction. A small acceleration means velocity is changing slowly, or over a long time interval. Like velocity, acceleration also has a direction. The more familiar case of acceleration is when motion is in just one direction, so that all that is changing is the speed. Here are some examples of acceleration:
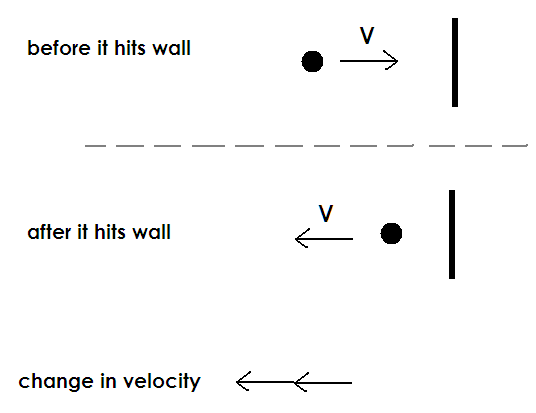When a ball bounces off a wall, its speed might not change much but the direction of motion does. The change in velocity is large and is directed away from the wall. To figure the acceleration, we would divide the change in velocity by the (short) time it takes for the bounce—acceleration is huge! When the initial and final velocities are in different directions we have to learn how to do the arithmetic of numbers that have directions attached to them; for the purposes of this course we will only use a qualitative definition of acceleration: if a moving object veers to the right, it has accelerated to the right, whether its speed has changed or not. If it speeds up, it has a forwards (or positive) acceleration. If it slows down, it has a backwards (or negative) acceleration.
Force
A force is a push or pull. We can't see forces, but we can see and feel their effects. They come in all sizes, and we can measure them. We encounter several kinds of forces every day.
*The earth exerts forces on everything, due to gravity. The size of the earth’s gravitational force on an object is called the weight of the object.
*Magnets exert forces on each other while they are still several centimeters apart.
*Running a comb through your hair charges it, creating an electrostatic force that enables it to pick up small pieces of paper.
*A spring or a rubber band exerts a force when it is stretched. When you let go of the rubber band, this force causes it to contract back to its original length.
*The sail of a ship deflects the wind, which causes a force on the sail that propels the ship.
*When an object slides on a surface, it encounters the friction force, which opposes the motion. Friction is easiest to explain in terms of energy: It represents a sharing of the mechanical energy of the moving object with the environment. A ball rolling on a soft surface also shares energy with the surface it is rolling on, and thus also encounters a kind of friction.
* A book sitting on a table experiences two forces: gravity and an upward force that prevents it from moving downward. We don’t need to know much about this response force. We can explain its existence because it prevents something from happening, and is as large as it needs to be to accomplish this; it’s bigger for a fish tank than it is for a book. In many cases it is simpler to ignore both this response force and any other forces that would cause the system being studied to do something that is being prevented. Thus a ball on a level table in effect does not experience gravity, because it can't move downward; a ball on an inclined surface experiences a force only along the surface, which is due more to gravity than to the ball’s weight (because motion along the incline takes it to a lower height but not directly downward).
When we weigh an object with a spring scale, gravity pulls it downwards, which stretches the spring in the scale. The scale is calibrated in newtons. The weight of 1 kilogram is 9.8 newtons (on earth); a newton is about 1/5 of a pound. Why don’t we use the weight of 1 kilogram as the unit of force? Because the gravitational force on an object varies from place to place, even on the earth, and we need a set of units we can use all over the universe. The weight of the standard kilogram mass in Paris, France is not exactly the weight of a kilogram in your town, and pretty irrelevant to the weight of a kilogram on the moon.
Since the scale is to be used to measure forces, we refer to it as a "force scale" rather than a "spring scale.".
Force is another quantity that has both a size and a direction. The gravitational force is downwards (by definition!) but we can use the force scale to determine how hard you have to pull to open a door. To be completely clear, we have to specify "who" is pulling on "what". Just weighing a rock allows us to define many different forces:
Some of these forces are upward, and some are downward. They are all the same size, in this particular system, for reasons to be explained below. For now, the point is that conceptually these forces are all distinct. We should recognize that they are all present, and when we talk about "the force in this system" we have to be clear about which one we have in mind.
Energy
Energy is what you have to add to make cold things warmer, slowly moving objects go faster, or to lift something up. In fact, energy has many forms. They are related by the requirement that when we change one form into another, the total energy of the universe stays constant. We say "energy is conserved."
There are many forms of energy. Here are some examples:
* An object has energy when it is moving ("kinetic energy"). The faster it moves, the more kinetic energy it has. Kinetic energy also depends on mass, so that for different objects moving at the same speed, heavy objects have more kinetic energy than light ones do.
*A book on a high shelf has gravitational energy, due to gravity It is frequently called "gravitational potential energy," where the word "potential" means that the energy is stored and can be released if the book falls off the shelf. Gravitational energy depends on the weight of the book and on how high it is. It is actually a property of the system that combines the book and the earth (just as the weight of the book actually depends on the earth being what it is). When the same book is lying on the floor, it has less potential energy, because it’s lower down.
*A stretched spring has more energy than the unstretched spring ("elastic energy").
*A hot object has more energy than when it is cold ("thermal energy").
*Wires deliver energy ("electrical energy").
*A chemical fuel (such as coal or gasoline) releases energy when it is burned ("chemical energy").
A first step in coming to understand the world is to be able to recognize the various forms of energy.
Conservation of energy
Energy can be converted from one form to another, as when the elastic energy of a stretched bow is given to the kinetic energy of an arrow.
The basic fact about energy that makes this concept useful is that as energy is converted from one form into another, the total amount of energy in the universe does not change. We say: energy is conserved, and refer to the idea as the principle of conservation of energy. It puts limits on what can happen:
When we throw a ball straight up, we give it some kinetic energy. As the ball rises, its kinetic energy is decreasing. Eventually it will reach a height such that it has given up all of its kinetic energy, which means it has stopped rising. It can't go any higher, because it has no more energy to give to gravity.
Energy is conserved, and so the energy we gave to the ball is always somewhere. At first it is in the form of the kinetic energy of the ball, but as the ball rises it is transformed into gravitational energy. Some of it is given to the air while pushing it out of the way, but if we ignore this small correction, we have the result that the sum of kinetic energy and gravitational energy is constant as the ball moves.
This is relevant to other systems, too. Consider a coal truck, moving on a mountain road: it goes slowly at the tops of the hills, and rapidly in the valleys. Of course, there are many ways that the truck is losing energy to its brakes and wind resistance, and the engine is turning chemical energy into other forms to replace this -- but we can understand the relationship between speed and height by assuming that the sum of kinetic and gravitational energy is constant. In the valleys the gravitational energy is less and the kinetic energy is correspondingly greater. If the valley is deep enough, this coal truck will violate the 55 mph speed limit -- the laws of physics and the Laws of Kentucky disagree on what the coal truck should do!
Gravitational energy is frequently called "potential energy," because we can't see the energy in a heavy chandelier until it falls -- its potential danger is its potential energy. However, there are many ways to store energy – after all, it is conserved! – and whenever energy can be extracted from a system, it is "potential" energy. When physicists use the term, they are always referring to a system that is at least potentially reversible: all the energy put into a battery when we charge it can be extracted later.
Another way to store energy is to stretch a spring (or, more generally, bend, twist, or stretch an elastic material). In activity 10?, a kind of spring is used to launch a ball straight up. The amount of energy given to the spring is determined by its physical properties and by how far it is bent before it is released; since these are all constant, the ball always gets the same amount of energy. But then balls of different masses will have different speeds (to have the same kinetic energy), and will fly to different heights (to have the same gravitational potential energy).
The Laws of Motion
To understand how things move we need to understand the relationship between position and velocity, and between velocity and acceleration. Thus it is not a coincidence that Newton, who formulated the laws of motion, also played a major role in the development of calculus, which gives a precise definition of such concepts as instantaneous velocity and how it relates to acceleration. Physicists usually refer to Newton’s laws by number, using the order and even the exact words that Newton used to describe the laws. For teaching purposes, we prefer to give the three laws descriptive names with clearer statements, and present them in a different order than Newton chose.:
The Law of Inertia, Newton’s first law: An isolated object (that is, an object that is not interacting with anything else) will maintain constant speed and direction of motion.
In the real world, the Law of Inertia may seem abstract because everything is always touching something else. But we can come close to realizing the law by rolling a ball on a smooth track. Significantly, what we have done is to remove ways for the ball to interact with other things. Our "everyday rules of motion" seem to say that a moving object slows down because it is supposed to—as a property built into the object. According to the laws of physics, though, a moving object only slows down because something has interfered with it. This realization leads us to search for the cause outside the object itself.
Another way to state the Law of Inertia is: In the absence of external forces, an object will maintain constant velocity. (Velocity includes both speed and direction.) Objects that are not moving at all are also included in this law; if it’s not moving, it won't start to move unless a force makes it.
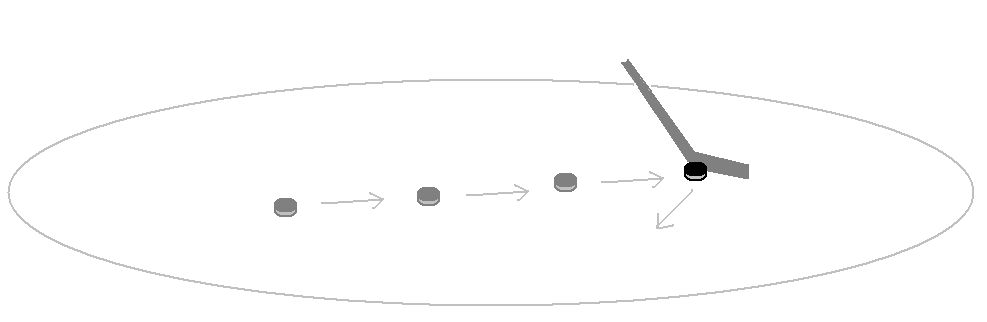
The Law of Inertia appears centrally in two activities: #5, We’re On a Roll, in which a ball rolling on a level track does not slow down (or at least, not much), and #6, Steering a Ball, which makes the point that a rolling ball moves in a straight line in the absence of external forces.
The Law of Interaction, Newton's third law: When object A exerts a force on object B, object B exerts an equal and opposite force on A.
This is a statement about interacting systems. Pairs of forces that are related this way are always equal and opposite, in any system, no matter what kinds of forces are involved, and even if the system is moving or accelerating. It is a completely general rule. The law implies that you can't pull yourself up by your shoelaces because the upward force you exert on the laces is exactly equal and opposite to the downward force your shoelaces exert on your hand.
As another example of the law of interaction, imagine taking your pet pig for a walk. When the pig balks and doesn’t want to move, you feel the force of the pig pulling back on you. At the same time, the pig feels exactly the same size force, but in the opposite direction.
Let’s return to the example of weighing a rock to see the interplay among these laws of motion. When we weigh a rock, the scale tells us the force acting on it, where what we wanted to know is the gravitational force on the rock. Earlier we identified the five forces in action:
A. the force of gravity on the rock
B. the force of the scale on the rock
C. the force of the rock on the scale
D. the force exerted at the top end of the scale to hold it in place (if we don’t hold the scale up, everything will fall down)
E. the force exerted by the scale on whatever is holding it up
These are related to each other as follows:
*The forces B and C (and also D and E) form a natural pair, because they are "the force of this on that" and "the force of that on this." According to the Law of Interaction, these forces are opposite in direction and equal in size.
*The forces A and B form a different kind of pair. These are forces acting on the same thing: the rock. They don’t have to be equal, but when they aren’t there would be an unbalanced force on the rock that would cause it to accelerate. So long as the system holds steady, forces A and B are equal. For the same reason, forces C and D are equal.
Thus the scale exerts a force on the object that balances the force of gravity, preventing the object from accelerating. The scale actually reports the force C that the object exerts on the scale. But C = B (Law of Interaction) and B = A (Law of Force and Acceleration), so the scale does tell us the weight of the rock.
If you try to weigh a rock while waving it and the scale around, you will see that the scale reads different values at different times; this means that the force of the scale on the rock is not the same as the force of gravity on the rock. The scale reading is C (the force of the rock on the scale), which is the same size as B (the force of the scale on the rock). This, however, is not equal to force A (the force of gravity on the rock, otherwise known as the weight of the rock) because the rock is accelerating, and now the scale reading is wrong. To understand this system fully, we need the Law of Force and Acceleration, the last of Newton’s laws.
The Law of Force and Acceleration, Newton’s second law: When a net force acts on an object, it accelerates in the direction of the force, according to the mathematical rule Force = mass x acceleration.
This law addresses what happens when any force acts on an object. If there is more than one force acting on the object, we combine them (noting the directions as well as the magnitudes of the forces) to get the net force on the object.
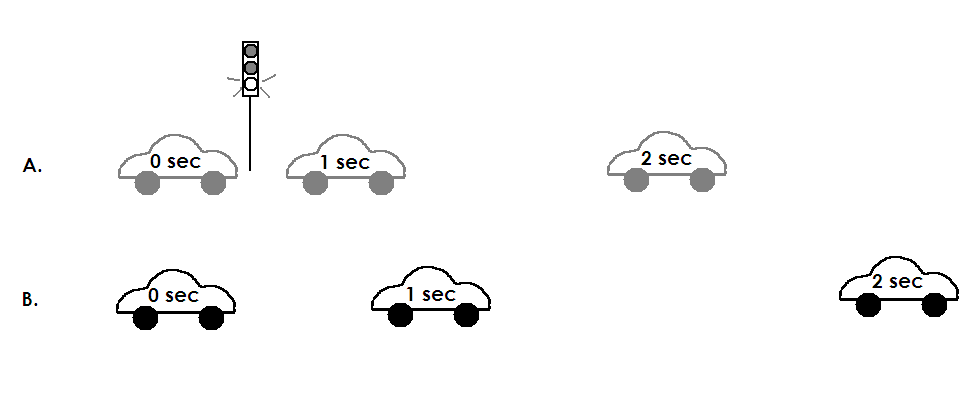
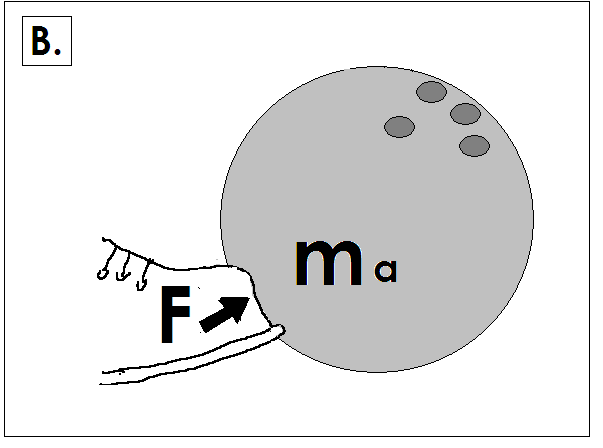
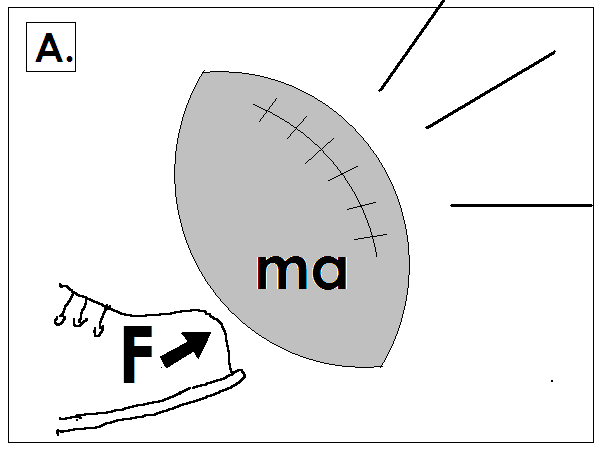
Force = mass x acceleration tells us it is easier to get a ping-pong ball moving (and easier to make it stop) than it is a watermelon. Because the watermelon has larger mass, it will take a larger force to achieve the same change in motion. The diagrams A. and B. show another example. The Law of Force and Acceleration explains why it is possible to kick a football and send it flying, but using the same force on a bowling ball makes it barely budge. The applied force (F, your kick) is equal both times, but the mass of the bowling ball is much larger than that of the football, so Force = mass x acceleration tells us that the bowling ball’s acceleration will be much smaller than the football’s acceleration.
The force unit has been chosen so that a 1 newton force will cause 1 kilogram to accelerate at 1 m/sec2
1 Newton = 1 Kg x 1 meter/second2
When you are riding along a highway at constant velocity, it is possible to adopt the point of view that you and the car are standing still and the world is rushing by. The moving point of view is fine, provided that the motion is constant in speed and direction. However, you should not to try to do physics from a point of view that is changing velocity. We will always discuss how a car goes around a curve from the point of view of someone standing by the road, and not from the point of view of the people in the car.
A falling rock gains speed because only the force of gravity is present. Its acceleration is in the direction of its motion. A satellite orbits the earth with constant speed but changing direction. It is accelerating downward (towards the earth, in the direction that it is veering), again due to the unbalanced force of gravity.
Having you discover the truth of the Law of Force and Acceleration for yourself is an important objective of this course. Much of this course is dedicated to establishing the concepts of velocity, force, and acceleration independently, because the Law of Force and Acceleration is incomprehensible until you clearly understand these. The Law of Force and Acceleration first appears in the activity, Steering a Ball, in which a ball is made to follow a curved path by exerting a lateral force on it. In the activity Acceleration On The Level, you will observe that a bubble level detects acceleration, and they will study the effects of applied forces on it. Activity 9, Soapbox Derby, shows that a ball subject to a constant unbalanced force has a constant acceleration.
Detecting and sharing energy
The rule that energy can neither be created not destroyed is not obvious, and was overlooked by scientists for a very long time. There are two reasons for this: some forms of energy are harder to detect than others; and once energy is shared with many different parts of a system, it's hard to get it back into its original concentrated (easier to see) form.
Some forms of energy are hard to detect
One form that is particularly hard to see is thermal energy. When you lift a brick above the floor, it has gravitational energy; you gave it some of our own energy in the process of lifting it. When you drop the brick, its gravitational energy is changed into kinetic energy as it falls. When it hits the floor, the energy does not disappear -- it has to go somewhere when the brick stops, and in this case it goes to heat. We are not down there under the brick to measure its temperature, but if we could do that, we would find a very slight increase in the temperature of the brick and the floor. The greater the starting height of the brick before the drop, the higher the temperature rise when it hits the floor. It takes a very large amount of energy to raise the temperature of a brick by 1 degree -- the equivalent of dropping the brick several hundred feet. It would be hard to measure the temperature rise, but it is nevertheless there.
For another example, there is a very large amount of chemical energy released when gasoline is burned, even though it resembles water, which will not burn at all. In view of these examples it is not surprising that we frequently get the impression that energy can be lost or gained.
Sharing energy
The second aspect that disguises the conservation of energy is that it tends to become shared among all the parts of a system, and once it is shared, it will not become reconcentrated. Thus a rolling ball shares its energy with the floor on which it moves, and comes to a stop; the reverse process of the ball that spontaneously speeds up will never happen. This aspect of energy is a whole long story in of itself, and so we will limit our discussion of it to the observation that kinetic energy naturally turns into thermal energy but not the other way around -- so for example, water only flows downhill.
Energy all around us
It is interesting and useful to analyze everyday events in terms of the flow of energy from one form to another. Here are a few examples:
Sunlight brings energy to the earth. Most of this is turned to heat. All of the energy of the weather -- wind, rain, flowing rivers -- is due to the uneven heating. Eventually this energy escapes in the form of invisible infrared light.
Some of the sun's energy is captured by growing plants, in the form of chemical energy. This stored sunlight is the energy we get from food, and also from any fuel we burn (the energy of oil and coal started as sunlight millions of years ago!).
People are machines to convert food energy into other forms, but they are not as simple, which again helps hide the principle of the conservation of energy. When we carry a box upstairs, we are supplying energy that becomes the increased gravity energy of the box. In principle, when we carry a box downstairs we should be able to gain energy from it and become less tired! But the human organism doesn't have the necessary mechanism to make the reverse transition, and the energy is all turned to heat. It should require no energy at all to hold a bag of flour or even to carry across a level floor, but we get tired doing it even though a grocery cart does not.
Measuring energy
Because there are many forms of energy, there are many ways to measure it.
*The metric unit of energy is the Joule, A Joule is the amount of energy needed to lift a 1 Newton object up 1 meter. Imagine lifting a plum (it weighs about 1 Newton) from the bottom of the refrigerator to the top shelf; you’ve just given it about 1 Joule of potential energy..
* On the electrical bill, energy is measured in Kilowatt-hours (KWhr), which is 3,600,000 Joules.
* On the gas bill it is measured in British Thermal Units (BTU). 1 BTU is 1054 Joules.
* The energy in food is measured in calories (=4186 Joules). (however, the kind of calorie that you count is actually a kilocalorie = 1000 calories).
* When you buy energy at the gasoline pump, it is measured in gallons (about 150,000,000 J).
In this module, we will always use the Joule as the energy unit.
Force and Energy
One way to transfer energy to an object is to push on it. The further it goes while you are pushing, the more energy is required:
Energy transferred = Force x distance
where the "distance" is how far the object moves, while the force is being exerted. When the force is measured in Newtons and the distance, in meters, the energy is measured in Joules. For example, when you drop an egg, gravity is pulling downwards and the egg is moving downwards. The amount of energy transferred to the egg (visible in the form of its kinetic energy) increases as it moves, because the "distance" is increasing in the relation above. However, when you rollerskate down the hall, you don’t gain energy from gravity, even though there is both a force (your weight) and a distance involved – because the force and the motion are in different directions.
In mechanical systems it is generally possible to turn this relationship around: if energy is transferred while an object moves, there was a force acting. This point of view (joined with the conservation of energy) gives a simple analysis of a lever [diagram]: as the lever turns, the two ends move different distances, D and d. When we exert a force on one end, a different FORCE results on the other, related by
force x DISTANCE = energy transferred = FORCE x distance .
Newton’s Laws and Everyday Experience
We all have plenty of experience with how things move, and we carry around in our heads a set of rules:
These Laws of Everyday Motion describe the world we live in, where everything is in contact with other things, where gravity is a pervasive and constant influence, and where we try to interpret everything from our own point of view. The everyday world is too complicated to be a good place to start a study of motion.
Physics tries to understand the world by looking at simple, isolated systems. Moving objects slow down because they share their energy with other things; but we can greatly decrease this interaction by using smooth surfaces, lubrication, bearings, or by rolling instead of sliding. The gravitational force is always present, but it has no effect on the motion of an object along a horizontal surface. A person may get tired holding a box of bricks, but a table will not. An important part of the simplification is recognizing the part of motion that involves properties of the an object (such as mass, velocity, acceleration), and the part that is due to its interactions with everything else (forces). This leads to a better description of the world, which can equally well describe and explain the motions of planets and porch swings and grocery carts and galaxies.
Having the students discover the truth of the Law of Motion for themselves is the central objective of the module. In activity #8 Rolling Down Hill, Again it is discovered that a ball subject to a constant unbalanced force has a constant acceleration; in activity #9 On The Level, the students will observe that a level detects acceleration, and study the effects of applied forces on it. Here connection will be made to activity #6 Steering a Ball, in which a ball is made to follow a curved path by exerting a lateral force on it. Finally, activity #12 Understanding the Pendulum provides a context in which to discuss force and accelerated motion.
Resisting the temptation to tell the whole story at once, we had to ignore some aspects of the early activities (in Activity 5 a ramp was used to produce moving balls without asking "What happens to the ball on the ramp?"; in Activity 6, the guide walls "interfere" with the motion of the ball, while in fact they are exerting a lateral force on the ball; in Activity 7 we studied the acceleration of a ball on an incline without asking why the ball would accelerate).