A ball rolling on a table top can be going in any direction. To predict where the ball will be later, we have to specify the velocity, which is the concept that contains both the speed and the direction. For example, the ball can be going northeast at 1 m/sec, or south at 2 m/sec.

In the previous units, the ball was constrained to move along a track. Even here, the motion can be to the right or to the left. If we calculate the velocity from
   velocity = (final coordinate - initial coordinate)/time
We will get a positive number when the ball is going one way, and a negative number when it is going the other way. Then "1 meter per second to the left" can also be reported as "-1 meter per second to the right."

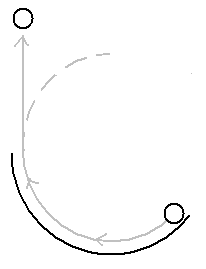
In the activity "Steering the Ball" the first observation is that the ball tends to go in a straight line. This observation is the Law of Inertia: an object will have constant velocity when no force acts upon it -- that is, it will travel in a straight line at constant speed. Unfortunately, in everyday experience there are always forces acting, such as gravity and frictional forces, so that it seems that moving objects always slow down and hardly ever go where they are originally directed. However, a ball rolling on a smooth, horizontal surface is a good approximation to the case that the law describes: it moves in a straight line, and doesn't slow down very rapidly. If we want the ball to go anywhere else, we have to interfere with its motion, by somehow exerting a force on it. In the case of this activity, the ball only changes direction while there is a wall to guide it, and as soon as it leaves the wall, it continues in a straight line. The ball does not "learn" to move in a curved path.

The Law of Inertia affects us in many ways, but frequently is not recognized. For example, as a bus comes to a stop, the standing passengers fall forwards. From their point of view, it seems that there was a force that suddenly pushed them forwards, but from the point of view of someone outside the bus, it was just that the moving passengers continued to move at constant speed, as dictated by the law of inertia, while the bus stops. There is no push on the people; the perception that there is one comes from ignoring the change of motion of the bus. The riders imagine that the bus is not moving at all, and since they find themselves suddenly moving forward relative to the bus, it seems that a force must have been exerted on them.

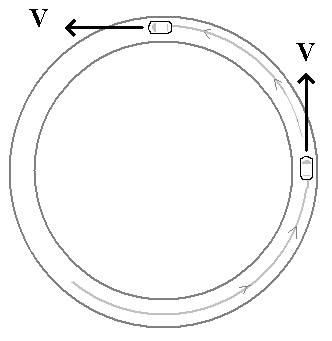A similar thing happens to the passengers in a car that is going around a curve. The car follows a curved path. Were it not for their seat belts, the people in the car would obey the law of inertia, and would move with constant speed and direction -- right off the road. From the point of view of the passengers, it seems that there is a force pulling them outwards; but this is again a consequence of ignoring the motion of the car.

Graphs of motion