A pendulum consists of a weight that must travel on a circular arc that is determined by the length of the string. It swings back and forth; it is also a little higher at the ends of the swing than it is at the middle. There are two ways to think about its motion:

The role of energy The pendulum has two kinds of energy: kinetic energy (when the weight is moving), and gravitational potential energy (because the circular path curves upwards). When we pull back the pendulum we are giving it some energy, and in the subsequent motion the energy is transferred back and forth from one form to the other. The pendulum returns to the same height on each end of the swing (except that each swing gets a little air moving, which is energy lost to the pendulum itself).

The maximum speed of the pendulum (at the middle) is related to the maximum height (at the ends) by conservation of energy. Since the kinetic energy and the gravitational potential energy are both proportional to the mass, the maximum speed of the pendulum is determined by the distance that it is pulled back, independent of the mass. We can estimate the period of the pendulum (the time it takes to swing) by dividing the distance it is pulled back by the maximum speed), and according to the argument just given, this does not depend on the mass of the pendulum.

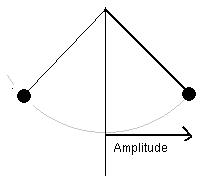
The maximum speed will be larger when the weight is pulled back further. Thus it is possible that a larger initial displacement will cause the period to increase (because the pendulum has farther to go) or decrease (because it is going faster) or stay the same (if the two effects exactly cancel out). For "small" displacements (which turns out to mean displacements of less than 60 degrees away from the vertical!), the period is in fact independent of the amplitude, this is a special property of the circular path of the pendulum.

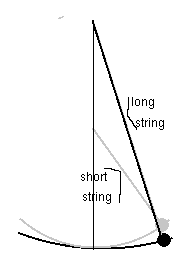
Changing the length of the string changes the circular path. Making the string longer means that for the same displacement, the weight is not lifted as much, and thus has less energy. So the maximum velocity is less and it takes longer for the pendulum to swing.

The role of force and acceleration The motion of the pendulum along the curved path is similar to the motion of a rolling ball on an incline: it experiences an unbalanced force that is proportional to the steepness of the incline, and this causes the weight to accelerate. It was observed in the unit on acceleration that the acceleration of a rolling ball does not depend on the mass, and this feature remains true here, too. However, the present situation is more complicated because the steepness varies as the ball moves. The acceleration is largest at the maximum displacement and decreases smoothly until the weight is at the center; thereafter, the pendulum is moving uphill and is decelerating.

With larger displacement, we get a greater steepness of the path and a larger initial acceleration; this again gives a larger maximum velocity.

Making the string longer decreases the steepness of the path at any displacement. Then the acceleration is less (just as in the unit on acceleration); the velocity will be less, and the period will be longer.