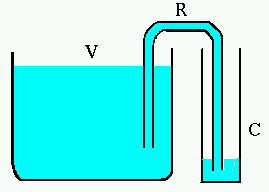
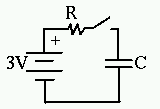
Let's compare a siphon system to an electrical circuit.
|
When we start the siphon, the tank will start filling the bottle on the right. The size of the current is determined by the properties (length and diameter) of the siphon tube. Eventually the bottle will fill up to the same level as the tank, but it could take a long time if the tube is long and thin. |
|
When we close the switch in this circuit, the battery will start pushing electricity into the capacitor. The size of the current is determined by the resistor. Eventually the capacitor will charge up, but it could take a long time if the resistance is large. |
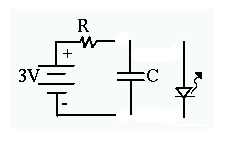Let's verify the analogy proposed here. Start with a pair of
batteries in series (to make 3V) and the
10 ohm 
resistor
connected to one end of the battery as shown in the diagram.
Use this combination to charge the capacitor for 1 second, and then
see if the capacitor is
able to cause the bipolar LED to light, using the capacitor as if it were a battery. If
not, use the battery-resistor combination to charge the capacitor for
several seconds more, and then try again. In
this way, get an estimate for how long it takes to charge the
capacitor using this resistor.
Then replace the 10 ohm resistor with the 100 ohm resistor
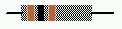, discharge the capacitor, and again determine
the charging time.
How do your results differ? Which
resistor is like a thick siphon tube, and which is like a thin
one?