Energy and the Tow Truck

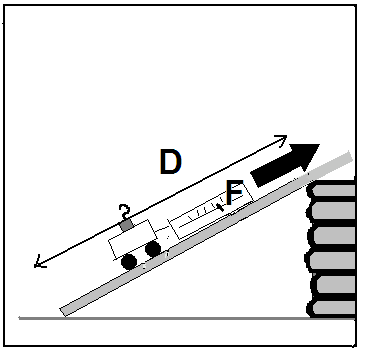
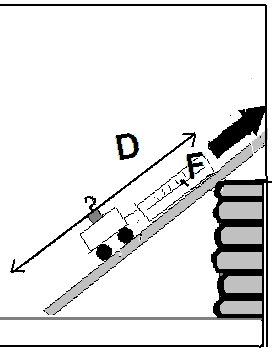
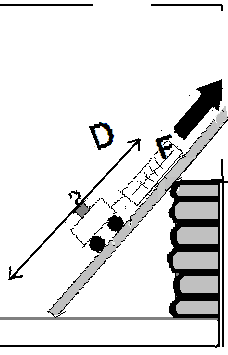
 We can move a cart to to a higher level using a steep incline, or one that is not steep at all. Do the different ways to lift the cart require different amounts of energy?

Materials

Set up a stack of books or a box about 30 cm high. This represents a hill. We want to get the cart to the top of the hill, using a ramp. We ramp can be gradual, or steep.
Measuring the force and the distanceA steeper ramp A still steeper ramp
We saw in the previous unit that the force needed to pull the cart up the ramp depends on how steep it is, but it also effects how far you have to pull it. What effect does this have on the energy required?

Calculating energy

It takes energy to lift something. The amount of energy you have to transfer to the object depends on how hard you have to pull (the Force) and how far you move it (the distance) in the direction of the force.

Energy = Force (in Newtons) x Distance (in meters).

The force and the distance must be in the same direction. The diagram shows the quantities we need to measure. Note that the part of the board that extends beyond the top of the hill doesn't count, and the height of the hill remains fixed. The units of energy are Joules. 1 Joule = 1 Newton x 1 meter


1. For three steepnesses of the ramp, measure the force needed to hold the cart on the ramp and the distance the cart must go along the ramp to get to the top of the hill, and calculate the corresponding energy.
 
F
(Newtons)		  
D
(meters		 Calculate energy
E = F x D
(Joules)
   
   
   
   

 

2. Another way to get the cart to the top of the hill is to lift it straight up. Now the force is the weight of the cart, and the distance is the height of the hill. Add this line to your table.

 


3. According to your table, what effect does the steepness of the ramp have on the amount of energy needed to lift the cart to the top of the hill?

Check the box when you are done:   

Energy and levers