Research

We are enthusiastic about investigating the properties of materials with strong electron-correlation and spin-orbit interaction. This motivation is related to the history of condensed matter physics. There have been several paradigm shifts concerning our understanding of the state of matter. The state of matter was initially thought to be governed by its building blocks (i.e., atoms) and how these building blocks are bonded to one another (i.e., crystal structures). However, many properties of materials were found to change 'spontaneously' as external conditions or parameters (e.g., temperature, magnetic field, pressure, etc.) were varied – even if the structures and atoms remained the same. These phenomena were termed 'phase transitions.' Since their discovery, novel concepts related to phase transitions such as spontaneous symmetry breaking and order parameters were established.
We are currently witnessing another paradigm shift, ushering in a new era of condensed matter physics. The discovery of the quantum Hall effect in two-dimensional electron systems has led to the new idea that the state of matter is governed by not only crystal structure or symmetry but also the presence of topological invariants. This means that the quantum wavefunctions are tied in a knot. For example, the phase of a superconducting wavefunction varies smoothly from place to place, but in making a circuit around a ring it may end up different by a multiple of 2π. These different states of the superconductor carry different currents and are robust against external disturbance. Moreover, the topological invariants can be broken at points or lines, which can bring about new collective excitations (i.e., quasi-particles), leading to new physical properties. Such topologically-protected states of matter can provide a pathway to many useful device applications. Hence, the topological properties of matter are attracting attention not only in the condensed matter physics community but also in other areas of science and engineering.
Recent studies on 4d and 5d transition-metal oxide (TMO) crystals have revealed novel ground states resulting from the interplay between strong electron-correlation and the relativistic spin-orbit interaction. Such strong spin-orbit coupling is also believed to provide topologically-protected novel electronic states, leading to an exciting new field of condensed matter physics. Therefore, the unique circumstance of coexisting strong electron-correlation and spin-orbit coupling in 4d and 5d TMOs has attracted enormous interest in these compounds.

1. Why do we study thin-films and heterostructures?

There has been much experimental work dedicated to finding topological phenomena in oxide crystals including ruthenates and iridates. However, topological properties have not been clearly observed due to correlation-induced magnetic ordering and fully-gapped insulating ground states. We have noted that the topological invariant of a system is governed by two essential ingredients, the dimensionality and the symmetry of the system. In one or two dimensions, unwanted magnetic ordering can be suppressed by enhanced quantum fluctuation of the order parameters, making hidden topological states visible. Hence, if we can increase the quantum fluctuation of a system by lowering its dimensionality or changing its symmetry, the hidden nontrivial topological states may emerge. Our approach is to make model low-dimensional systems from thin films. This protocol offers further benefits of tunability for controlling the dimensionality, the lattice-symmetry (by strain), and the interfacial interactions. Tuning these parameters is expected to compel strongly interacting electrons in complex oxides to exhibit unprecedented exotic collective states. Moreover, since topological materials undergo phase transitions as these parameters are varied, the tunability of this approach offers capabilities to fully investigate the phase diagrams of topological states.

2. One-dimensional quantum-stripe superlattices

We developed a new approach for controlling the dimensionality of complex oxide superlattices between one dimension (1D) and two dimension (2D),which offers a new direction of oxide quantum materials. As a prototype material, we have found that one dimensional (1D) structural and electronic confinement can be experimentally achieved for iridate superlattice systems, as shown in figure. This superlattice method can be extended to any two dimensional (2D) layered material and thereby allows for tunability between 1D and 2D. See Advanced Materials 29, 163798 (2017) for details.

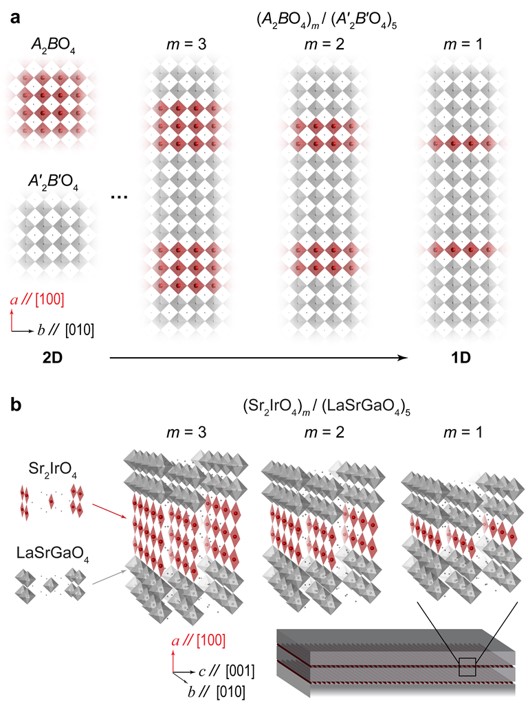
[Figure] Schematic diagrams of turning a 2D layered material into a 1D quantum stripe superlattice.
a) The leftmost panel shows the in-plane structures of two transition-metal oxides, A₂BO₄ (top) and A'₂B'O₄ (bottom), with the K2NiF4 symmetry. Each red (gray) square contains transition-metal ions B (B') at its center and an oxygen atom at each of its four vertices.
b) Schematic diagrams of a-axis-oriented (Sr₂IrO₄)_m/(LaSrGaO₄)₅ superlattices for m = 3, m = 2, and m = 1 for realizing the low-dimensional quantum stripes of IrO₂ (red squares) on LaSrGaO₄ (100) substrates. The 1D IrO₂ stripes run parallel to the b-axis and are dimensionally confined by the wide-bandgap LaSrGaO₄ layers (grey octahedra).

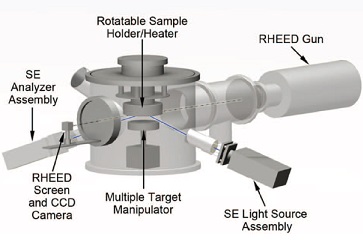
3. In-situ, real-time spectroscopic ellipsometry on complex oxide heterostructures

We have developed a pulsed laser deposition (PLD) system with dual in-situ capabilities for optical spectroscopic ellipsometry and reflection high-energy electron diffraction (RHEED). Spectroscopic ellipsometry uses a range of photon energies from 1.2 eV – 6.0 eV (1000 nm – 210 nm in wavelength). This spectral range allows us to monitor the real and imaginary dielectric functions of thin films and heterostructures in real time, which greatly complements the structural information obtained by RHEED (see Review of Scientific Instruments 84, 043902 (2013) for technical details). The dual in-situ monitoring of both spectroscopic ellipsometry and RHEED provides considerable freedom since the former is not restricted by the growth conditions, whereas the latter has a limited operational range of background gas pressures.